In the vast realm of mathematics, the concept of proportion, with its intricate relationships between quantities, assumes a pivotal role. Acting as a fundamental principle, proportion governs both real-world problems and abstract mathematical equations. Understanding proportion is not only crucial for maintaining balance but is also indispensable for ensuring coherence in various mathematical scenarios. In this exploration, we will delve into the definition of proportion, its applications in mathematics, the different types it encompasses, and the crucial role of maths tuition in mastering this fundamental concept.
Defining Proportion:
Proportion, in its essence, is the relationship between two or more quantities that maintains a constant or consistent ratio. This relationship signifies balance and equality between different parts of a whole. In a proportion, the ratios of corresponding elements are equal, forming the foundation for solving a myriad of mathematical problems. The concept is deeply ingrained in various mathematical fields, providing a framework for solving equations and establishing connections between variables.
How to Apply Proportions in Mathematics:
The practical application of proportions in mathematics is extensive, encompassing scenarios ranging from fundamental problem-solving to intricate mathematical models. The utilization of proportions becomes particularly apparent when considering real-world examples. Let's explore a common application through the lens of a recipe, illustrating the importance of understanding and applying proportions.
Consider a baking recipe that requires a certain ratio of flour to sugar. The recipe calls for 2 cups of flour for every 1 cup of sugar. To determine how much flour is needed when using 3 cups of sugar, we can set up a proportion:
Flour/sugar = 2/1
Now, to find the amount of flour (flour) when using 3 cups of sugar (sugar), we cross-multiply to obtain:
Flourx 1 = 2 x 3
This simplifies to flour = 6 cups.
This example illustrates the application of proportions in a real-world context, showcasing how an understanding of proportionality ensures the right balance of ingredients in a recipe. The principles employed here are foundational to solving a wide range of mathematical problems, and they underscore the significance of proportion in practical scenarios.
Types of Proportion:
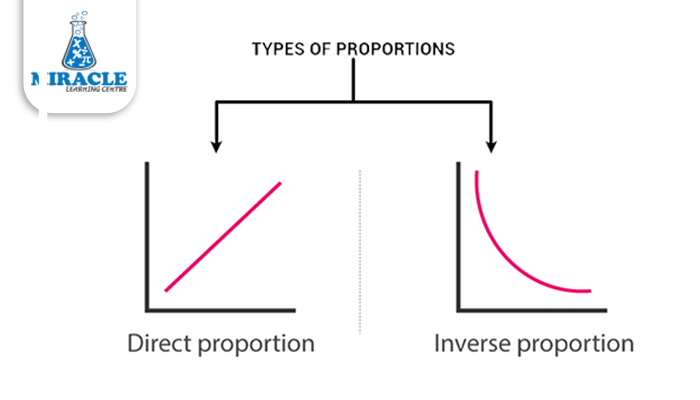
Proportions manifest in various forms, each addressing different relationships between quantities. The three primary types of proportion are direct proportion, inverse proportion, and continued proportion.
- Direct Proportion:
Direct proportion occurs when one quantity increases or decreases in proportion to another. In other words, if one variable doubles, the other variable also doubles. This relationship can be expressed through the equation y = kx, where 'k' is the constant of proportionality. For instance, if the time it takes to complete a task is directly proportional to the number of workers employed, doubling the number of workers will halve the time required to finish the task.
- Inverse Proportion:
Inverse proportion involves a scenario where one quantity increases as the other decreases, and vice versa. This relationship is represented by the equation xy = k, where 'k' is the constant of proportionality. An example of inverse proportion is the relationship between speed and time. If the speed of a vehicle is inversely proportional to the time taken to cover a certain distance, doubling the speed would result in halving the time taken to travel the same distance.
- Continued Proportion:
In continued proportion, three or more quantities are related in such a way that the ratio of the first to the second is the same as the ratio of the second to the third, and so on. This type of proportion is often encountered in more advanced mathematical contexts and problem-solving scenarios. An example of continued proportion is the sequence 2:4::6:12, where the ratio of 2 to 4 is the same as the ratio of 6 to 12.
Difference between Ratio and Proportion:
In mathematical discourse, the terms "ratio" and "proportion" are often used interchangeably, but they carry distinct meanings.
Definition:
- Ratio: A comparison of two or more quantities, expressing the relationship between them.
- Proportion: A specific type of ratio where the equality of two ratios is emphasized.
Representation:
- Ratio: Expressed as a fraction, such as a/b or a:b.
- Proportion: Written as an equation, often in the form of a/b = c/d.
Scope:
- Ratio: A broader concept, representing the relative size or magnitude of one quantity concerning another.
- Proportion: A subset of ratios, specifically addressing scenarios where two ratios are equal.
Nature of Relationship:
- Ratio: Describes the quantitative relationship between two or more quantities.
- Proportion: Highlights the equality of two ratios, emphasizing balance and consistency.
Application:
- Ratio: Used in various contexts, from expressing simple comparisons to more complex mathematical relationships.
- Proportion: Primarily employed when the equality of ratios is crucial, often in problem-solving involving constant relationships.
Understanding these distinctions is crucial for navigating mathematical problems effectively, providing clarity in both theoretical concepts and practical applications.
Why choose our maths tuition to learn it?
Our specialized Maths Tuition, led by experienced Maths Tutors in Singapore, offers a tailored and comprehensive approach to mastering proportions. With personalized attention and expert guidance, our Maths Tuition ensures a structured learning experience that aligns with individual needs.
Our skilled Maths Tutors in Singapore adeptly break down complex concepts, fostering a deeper understanding of proportions before advancing to more intricate applications. The interactive learning environment not only instils confidence but also equips students with the skills to confidently apply their mathematical knowledge.
Choose our Maths Tuition in Singapore for a solid foundation and a transformative learning journey with dedicated Maths Tutors.
Conclusion:
In conclusion, proportion stands as a cornerstone in mathematics, offering a systematic approach to understanding quantity relationships. Whether applied to real-world problems or abstract models, proportions maintain balance. Grasping diverse proportion types, mastering applications, and distinguishing ratio from proportion unlock the full potential of this mathematical principle. Specialized maths tuition enhances learning, ensuring a solid foundation in proportions and their applications.








